Suites numériques - Tableurs, Calculatrices

Mettre en oeuvre des algorithmes permettant de calculer un terme de rang donné
Mettre en oeuvre des algorithmes permettant de calculer une liste de termes de la suite
Savoir calculer le premiers termes d'une suite à partir d'une formule récursive ou explicite
Représentation graphique d'une suite

Dans chaque partie, nous raisonnons sur des exemples concrets de suite. Une fonction $f$ sera proposée dans chaque partie.

ICalcul direct sur calculatrice

Cette partie répond à la question : "comment calculer rapidement les premiers termes d'une suite à l'aide de sa calculatrice ?"

1Suite définie explicitement

On pose $u_n = \sqrt{3 n + 2}$ pour $n \in \mathbb{N}$.

Afin de calculer le terme $u_0$ de rang $0$ sur une calculatrice graphique, on tape
√(3*0 + 2)
On peut calculer les termes suivants sans retaper toute la formule :

CASIO

On remonte dans le calcul précédent à l'aide des touches de direction ↑

2Suite définie récursivement

Soit $(u_n)$ une suite définie récursivement pour tout $n \geq 0$ par : $$ \left\{ \begin{array}{lll} u_{n+1} &=& \sqrt{2 u_n + 3} \\ u_0 &=& 1 \end{array} \right. $$

La méthode suivante marche sur n'importe quel type de calculatrice graphique :

On va utiliser une variable de la calculatrices

pour mémoriser chaque terme succéssif de la suite, en partant du premier $u_0 = -1$ :

On commence par mémoriser la valeur initiale dans la variable A en tapant
1 → A
Il faut calculer $\sqrt{2 u_0 + 3}$ pour obtenir $u_1$. De plus, on le mémorise dans la variable A :
√(2*A+3)→A

On obtient la valeur $u_1$, qui remplace l'ancienne valeur $u_0$ dans la variable A.

Il faut calculer $\sqrt{2 u_1 + 3}$ pour obtenir $u_2$ et le mémoriser dans A : il n'y a qu'à taper le même calcul
√(2*A+3)→A

Cela fonctionne car la valeur de A a changé. On obtient donc $u_2$. Il n'y a qu'à rappeler le même calcul autant de fois que nécessaire pour calculer les premiers termes de la suite, comme le représente le shéma ci-dessous :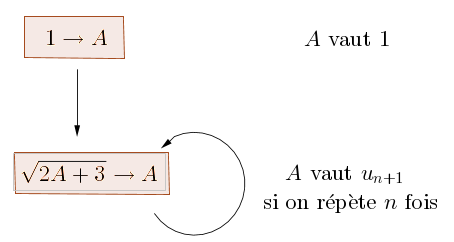

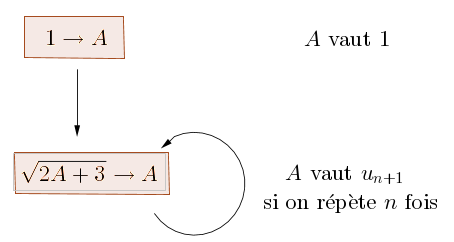
IIOutils de type tableur

Appuyer sur la touche menu et choisir Recur .
Pour entrer une formule explicite, il faut choisir le type avec F3 puis an avec F1 : La formule explicite à côté de an= Le rang de départ à celui de fin dans set (ou rang ) avec F5 Ci contre, on entre l'exemple suivant : $u_n = \frac{1}{n}$ pour tout $1 \leq n \leq 10$	Si on choisit de commencer à $n=0$ ici il y a une erreur.
Pour entrer une formule récursive, il faut choisir le type avec F3 puis an+1 avec F2 : La formule récursive à côté de an+1= Le rang de départ à celui de fin dans set (ou rang ) avec F5 La valeur de départ ao dans set Ci contre, on entre l'exemple suivant : Pour $0 \leq n \leq 10$ : $ \left\{ \begin{array}{lll} u_{n+1}&=&2 u_n\\ u_0&=&1 \end{array} \right. $

On peut lire les valeurs dans le tableur

(à partir de

Recur

$$ u_n = \frac{1}{n}$$

$$ \left\{ \begin{array}{lll} u_{n+1}&=&2 u_n \\ u_0&=&1 \end{array} \right. $$

IIITracer un nuage de points

1Calculatrice Casio

On va tracer le nuage de points de la suite définie explicitement par $u_n = \frac{1}{n}$ pour $1\leq n \leq 10$

Avant de tracer les points, il faut paramétrer la fenêtre. Depuis le menu

Recur

, faire

pour entre dans V-Window.

Xmin
et
Xmax
sont les bornes de l'axe des abscisses. On peut mettre le premier et le dernier indice de la suite ou un peu plus large.
Ymin
et
Ymax
sont les bornes de l'axe des ordonnées. Il vaut les choisir par rapport à la plus grande valeur et la plus petite valeur des $u_n$.

Ici comme on trace les 10 premières valeurs de $u_n=\frac{1}{n}$, on choisit :

$Xmin = 0$, $Xmax = 10$, $Ymin = 0$, $Ymax = 1$

Pour tracer le nuage de points, aller dans la table avec

, puis G-PLT avec

Appuyer sur la touche menu et choisir Recur .
Pour entrer une formule explicite, il faut choisir le type avec F3 puis an avec F1 : La formule explicite à côté de an= Le rang de départ à celui de fin dans set (ou rang ) avec F5 Ci contre, on entre l'exemple suivant : \(u_n = \frac{1}{n}\) pour tout \(1 \leq n \leq 10\)	Si on choisit de commencer à \(n=0\) ici il y a une erreur.
Pour entrer une formule récursive, il faut choisir le type avec F3 puis an+1 avec F2 : La formule récursive à côté de an+1= Le rang de départ à celui de fin dans set (ou rang ) avec F5 La valeur de départ ao dans set Ci contre, on entre l'exemple suivant : Pour \(0 \leq n \leq 10\) : \( \left\{ \begin{array}{lll} u_{n+1}&=&2 u_n\\ u_0&=&1 \end{array} \right. \)